Hypothesis Testing

• Shapiro Wilks
• One Sample T-Test
• Calculating Power
• Hypothesis Testing
• Sample Size Determination

## Data sample on chick weights
data(chickwts)
head(chickwts)

  weight      feed
1    179 horsebean
2    160 horsebean
3    136 horsebean
4    227 horsebean
5    217 horsebean
6    168 horsebean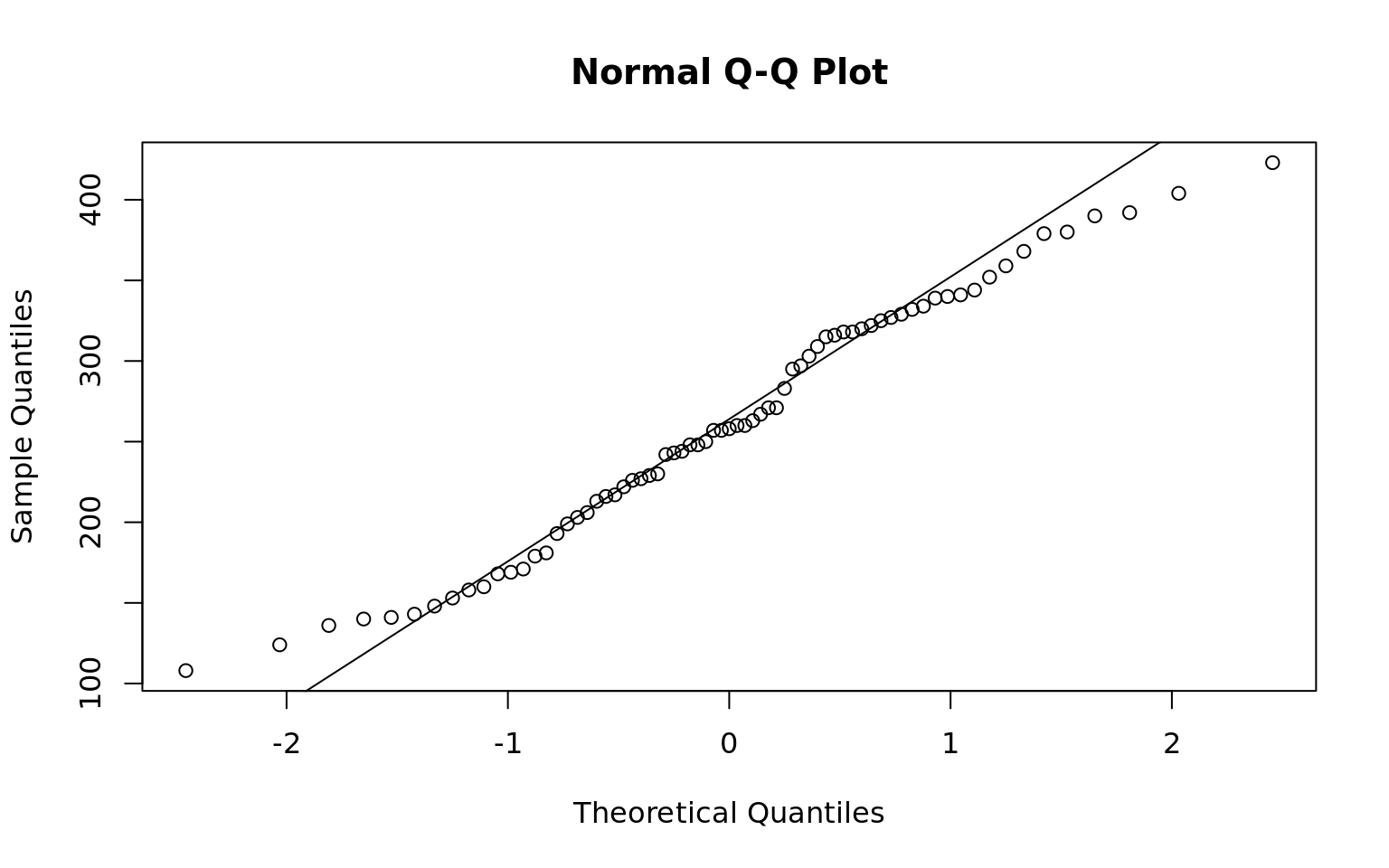

## Normal reference plot for height
qqnorm(chickwts$weight)
qqline(chickwts$weight)

## Are the data from a normal distribution?
shapiro.test(chickwts$weight)

    Shapiro-Wilk normality test

data:  chickwts$weight
W = 0.97674, p-value = 0.2101

mean(chickwts$weight)

[1] 261.3099

How does the sample mean compare to a hypothesis test that the true mean is < 260? What is the power of the test?

\[H_0: \mu \ge 260, H_a: \mu \lt 260\]

Population	Fail to Reject	Reject \(H_0\)
\(H_0\) is True	Correct	Type I Error
\(H_a\) is True	Type II Error	Correct

## What is the probability of a Type I error if we say the true mean is less than 250?
t.test(chickwts$weight, mu = 250, alternative = "less")

    One Sample t-test

data:  chickwts$weight
t = 1.2206, df = 70, p-value = 0.8868
alternative hypothesis: true mean is less than 250
95 percent confidence interval:
     -Inf 276.7549
sample estimates:
mean of x 
 261.3099 

## Verify the t statistic and p-value
(ts = (mean(chickwts$weight) - 250) / (sd(chickwts$weight) / sqrt(length(chickwts$weight))))

[1] 1.220623

pt(ts, df = 70)

[1] 0.8868377

## What is the probability of a Type I error if we say the true mean is > 245?
t.test(chickwts$weight, mu = 245, alternative = "greater")

    One Sample t-test

data:  chickwts$weight
t = 1.7603, df = 70, p-value = 0.04137
alternative hypothesis: true mean is greater than 245
95 percent confidence interval:
 245.8648      Inf
sample estimates:
mean of x 
 261.3099 

## Verify the t statistic and p-value
(ts = (mean(chickwts$weight) - 245) / (sd(chickwts$weight) / sqrt(length(chickwts$weight))))

[1] 1.760251

1 - pt(ts, df = 70)

[1] 0.04136678

## We have rejected the null hypothesis and said under an alpha of .05 there is enough evidence
## to suppor that the true mean of Chick Weights is > 245

## What is the power of our test?
power.t.test(n = length(chickwts$weight),
             delta = abs(mean(chickwts$weight) - 245),
             sd = sd(chickwts$weight),
             sig.level = .05,
             type = "one.sample",
             alternative = "one.sided", strict = TRUE)

     One-sample t test power calculation 

              n = 71
          delta = 16.30986
             sd = 78.0737
      sig.level = 0.05
          power = 0.5391727
    alternative = one.sided

## What sample size would we need to have a power of .8?
power.t.test(delta = abs(mean(chickwts$weight) - 245),
             sd = sd(chickwts$weight),
             sig.level = .05,
             power = .8,
             type = "one.sample",
             alternative = "one.sided", strict = TRUE)

     One-sample t test power calculation 

              n = 143.0323
          delta = 16.30986
             sd = 78.0737
      sig.level = 0.05
          power = 0.8
    alternative = one.sided

## Verify manually
(sd(chickwts$weight)^2 * (qnorm(p = .95) + qnorm(p = .8))^2) / abs(mean(chickwts$weight) - 245)^2

[1] 141.6698