VAR Modeling
library(vars)
# Generated Time Series
x1 = 10 + arima.sim(n = 100,model = list(order = c(1, 1, 1), ar = .1, ma = .2))
x2 = 10 + arima.sim(n = 100,model = list(order = c(1, 1, 1), ar = .1, ma = .2))
x3 = 10 + arima.sim(n = 100,model = list(order = c(1, 1, 1), ar = .1, ma = .2))
x4 = 10 + arima.sim(n = 100,model = list(order = c(1, 1, 1), ar = .1, ma = .2))
# Combine into a multivariate time series
x = data.frame(x1, x2, x3, x4)
# Create a variable auto-regression modle
mdl = VAR(x)
# Model summary
summary(mdl)
VAR Estimation Results:
=========================
Endogenous variables: x1, x2, x3, x4
Deterministic variables: const
Sample size: 100
Log Likelihood: -554.174
Roots of the characteristic polynomial:
1.001 0.9732 0.9732 0.8473
Call:
VAR(y = x)
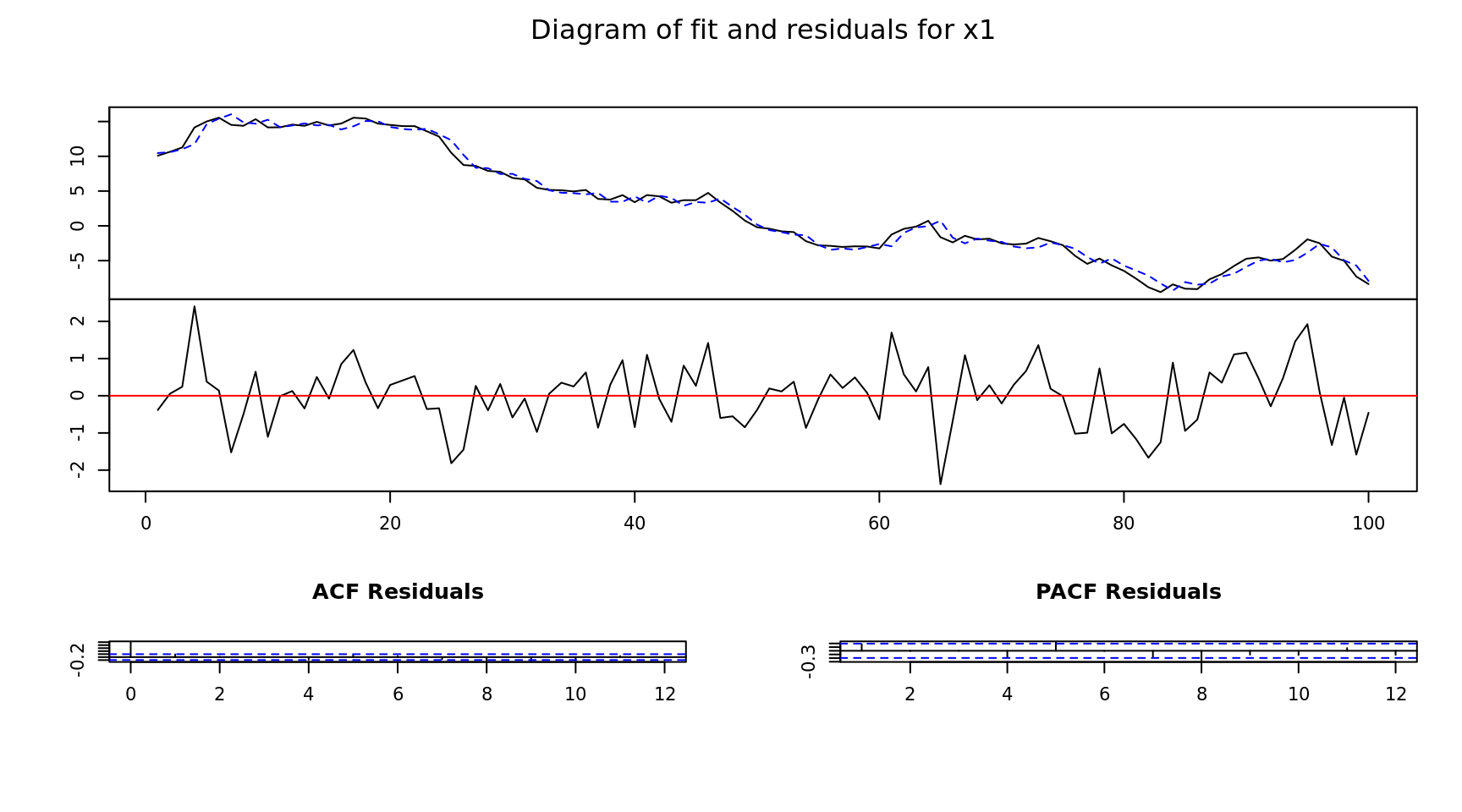
Estimation results for equation x1:
===================================
x1 = x1.l1 + x2.l1 + x3.l1 + x4.l1 + const
Estimate Std. Error t value Pr(>|t|)
x1.l1 0.963228 0.018160 53.040 < 2e-16 ***
x2.l1 0.075584 0.031008 2.438 0.01665 *
x3.l1 0.143179 0.043729 3.274 0.00148 **
x4.l1 0.007627 0.017186 0.444 0.65822
const -1.425166 0.584460 -2.438 0.01661 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.868 on 95 degrees of freedom
Multiple R-Squared: 0.9881, Adjusted R-squared: 0.9876
F-statistic: 1971 on 4 and 95 DF, p-value: < 2.2e-16
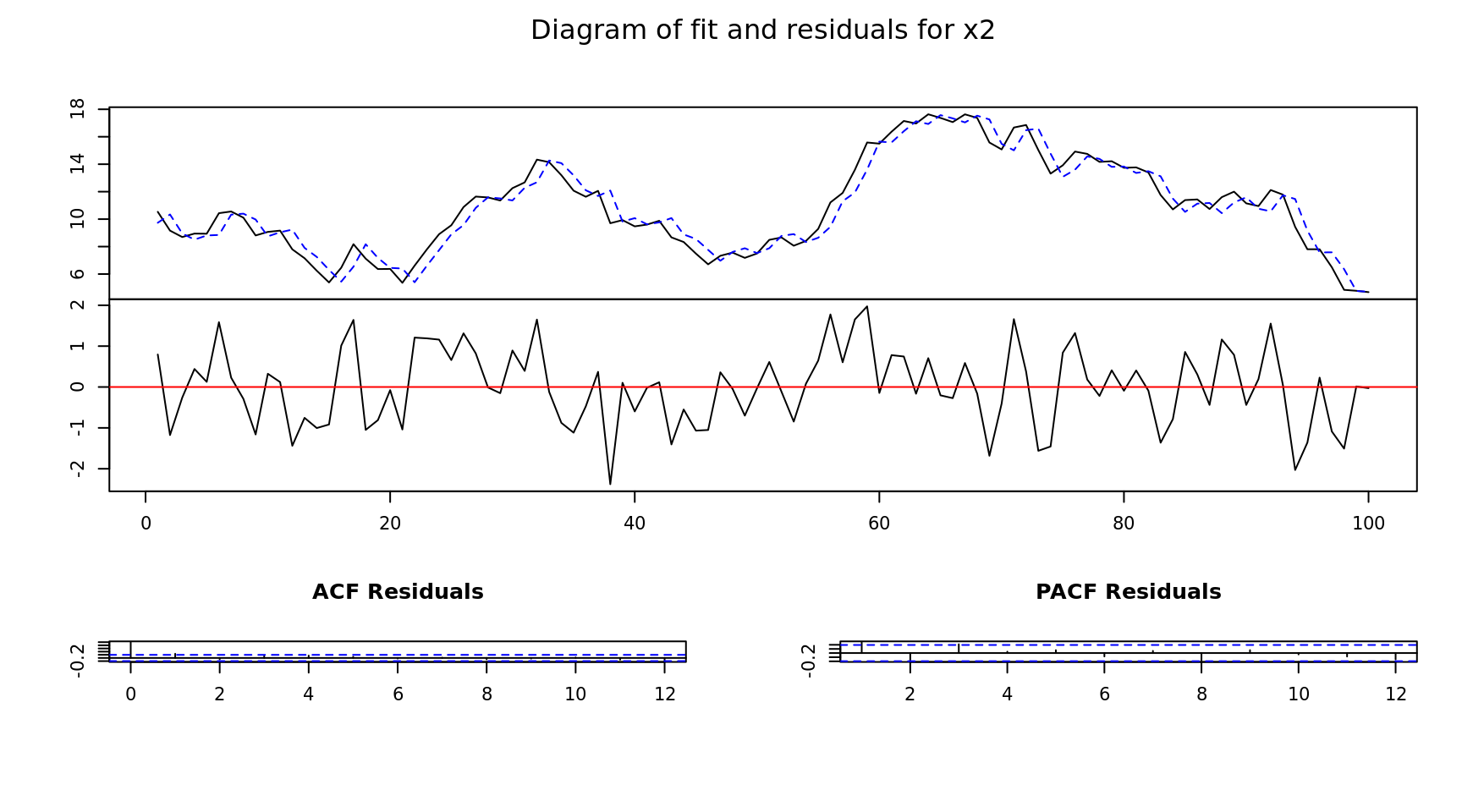
Estimation results for equation x2:
===================================
x2 = x1.l1 + x2.l1 + x3.l1 + x4.l1 + const
Estimate Std. Error t value Pr(>|t|)
x1.l1 -0.001462 0.019970 -0.073 0.942
x2.l1 0.972519 0.034098 28.521 <2e-16 ***
x3.l1 0.025001 0.048087 0.520 0.604
x4.l1 0.031043 0.018899 1.643 0.104
const -0.535590 0.642706 -0.833 0.407
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9545 on 95 degrees of freedom
Multiple R-Squared: 0.9251, Adjusted R-squared: 0.9219
F-statistic: 293.2 on 4 and 95 DF, p-value: < 2.2e-16
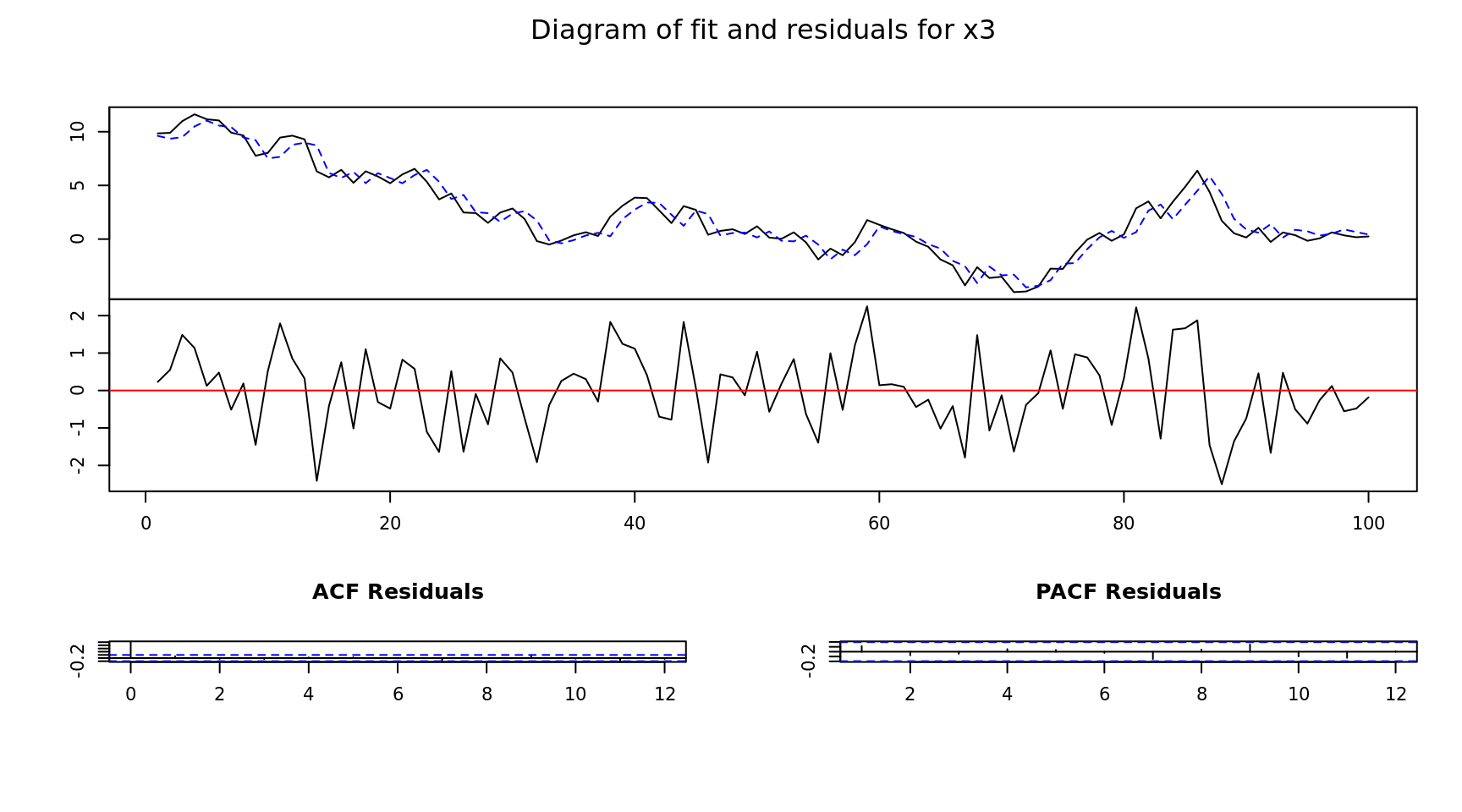
Estimation results for equation x3:
===================================
x3 = x1.l1 + x2.l1 + x3.l1 + x4.l1 + const
Estimate Std. Error t value Pr(>|t|)
x1.l1 0.02503 0.02235 1.120 0.2656
x2.l1 -0.01399 0.03816 -0.367 0.7147
x3.l1 0.85840 0.05381 15.951 <2e-16 ***
x4.l1 -0.04462 0.02115 -2.110 0.0375 *
const 1.36738 0.71927 1.901 0.0603 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.068 on 95 degrees of freedom
Multiple R-Squared: 0.929, Adjusted R-squared: 0.926
F-statistic: 310.8 on 4 and 95 DF, p-value: < 2.2e-16
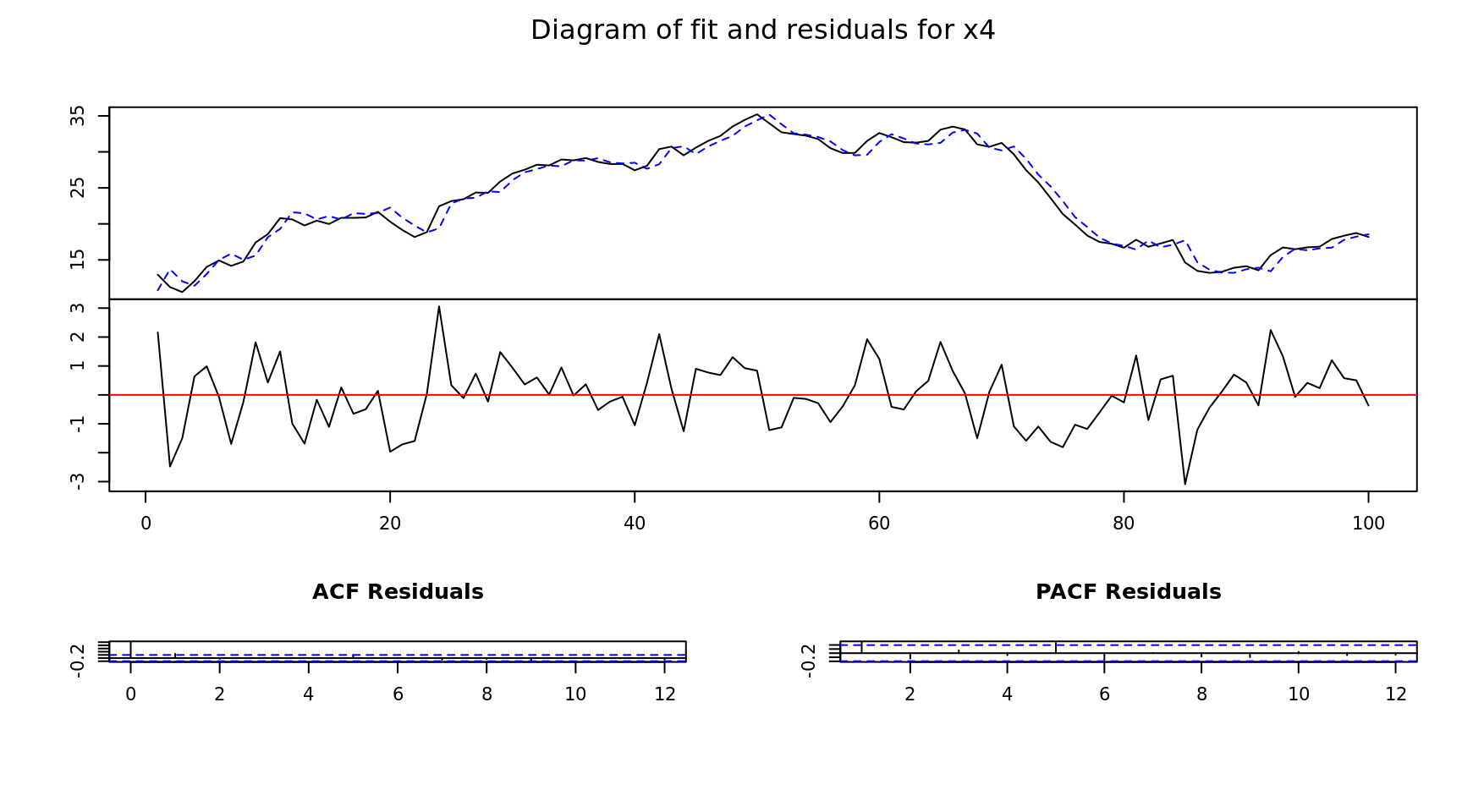
Estimation results for equation x4:
===================================
x4 = x1.l1 + x2.l1 + x3.l1 + x4.l1 + const
Estimate Std. Error t value Pr(>|t|)
x1.l1 0.01831 0.02364 0.774 0.441
x2.l1 -0.01214 0.04037 -0.301 0.764
x3.l1 0.07116 0.05693 1.250 0.214
x4.l1 0.99872 0.02238 44.633 <2e-16 ***
const 0.02153 0.76094 0.028 0.977
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.13 on 95 degrees of freedom
Multiple R-Squared: 0.9751, Adjusted R-squared: 0.9741
F-statistic: 930 on 4 and 95 DF, p-value: < 2.2e-16
Covariance matrix of residuals:
x1 x2 x3 x4
x1 0.75349 -0.09141 -0.01242 -0.05868
x2 -0.09141 0.91116 -0.06800 0.08389
x3 -0.01242 -0.06800 1.14116 -0.23538
x4 -0.05868 0.08389 -0.23538 1.27722
Correlation matrix of residuals:
x1 x2 x3 x4
x1 1.00000 -0.11032 -0.01339 -0.05981
x2 -0.11032 1.00000 -0.06669 0.07777
x3 -0.01339 -0.06669 1.00000 -0.19497
x4 -0.05981 0.07777 -0.19497 1.00000